Алгебраическая система

Алгебраическая система или алгебраическая структура, множество G (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Понятие А.с. родственно понятию универсальной алгебры.

n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество . По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).

Для А.с. естественным образом определяются морфизмы как отображения, сохраняющие операцию. Таким образом определяются категории групп, колец, R-модулейи т. п.

Если множество обладает структурой топологического пространства, и операции являются непрерывными, то его называют топологической А.с. Так, в топологической группе операции умножения и взятия обратного элемента являются непрерывными.

Не все алгебраические конструкции описываются А.с., в качестве примера иных можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними.

Список А.с.:

• Множество можно считать вырожденной А.с. с пустым набором операций и отношений.

Группоиды, полугруппы, группы

• Группоид — множество с одной бинарной операцией , обычно называемой умножением.

• Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение  имеет единственное решение для любых a и b.

• Квазигруппа — одновременно правая и левая квазигруппы.

• Лупа — квазигруппа с единичным элементом , таким, что .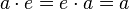

• Полугруппа — группоид, в котором умножение ассоциативно: .

• Моноид — полугруппа с единичным элементом.

• Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a−1, такой, что .

• Абелева группа — группа, в которой операция коммутативна, то есть, . Операцию в абелевой группе часто называют сложением ('+').

Кольца:

• Полукольцо — похоже на кольцо, но без обратимости сложения.

• Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)

• Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности: .

• Коммутативное кольцо — кольцо с коммутативным умножением.

• Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.

• Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.

• Поле — коммутативное кольцо, являющееся телом.

{-x^2+5x+2<2-4x {-x^2+21x-70>=5x-10

Алгебры:

• Алгебра (линейная) — пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой пространства

• Ассоциативная алгебра — алгебра с ассоциативным умножением

• Алгебра термов

• Коммутативная алгебра

• Градуированная алгебра

• Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым ), удовлетворяющим тождеству Якоби 

• Алгебра Лейбница — алгебра с умножением (обычно обозначаемым ), удовлетворяющим тождеству Якоби 

• Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности: 

• Алгебра некоммутативная йорданова — некоммутативная алгебра с тождеством слабой ассоциативности:  и тождеством эластичности: 

• Альтернативная алгебра — алгебра с тождествами 

• Алгебра Мальцева — антикоммутативная алгебра с тождеством

• Алгебра над операдой — один из наиболее общих видов А.с. Здесь сама операда играет роль сигнатуры алгебры.

Решётки:

• Решётка — структура с двумя коммутативными, ассоциативными, идемпотентными операциями, удовлетворяющими закону поглощения.

• Булева алгебра.

Лит.: П. Кон «Универсальная алгебра», — М.: Мир, 1969, 351 с А. И. Мальцев «Алгебраические системы», — М., Наука, 1970 г., 392 стр. с илл. «Общая алгебра, в 2-х томах (Серия: Справочная математическая библиотека)», В. А. Артамонов и др., под редакцией Л. А. Скорнякова, — М.: Наука, Физматлит, 1990—1991, 592 с + 480 с.