Algorithm

pp. 1  2  3

In mathematics and computer science, an algorithm  i/ˈælɡərɪðəm/ is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning. In simple words an algorithm is a step-by-step procedure for calculations.

Starting from an initial state and initial input (perhaps empty), the instructions describe a computation that, when executed, will proceed through a finite number of well-defined successive states, eventually producing "output" and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.

A partial formalization of the concept began with attempts to solve the Entscheidungsproblem (the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability" or "effective method"; those formalizations included the Gödel–Herbrand–Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church's lambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing's Turing machines of 1936–7 and 1939. Giving a formal definition of algorithms, corresponding to the intuitive notion, remains a challenging problem.

For a detailed presentation of the various points of view around the definition of "algorithm" see Algorithm characterizations. For examples of simple addition algorithms specified in the detailed manner described in Algorithm characterizations, see Algorithm examples.

While there is no generally accepted formal definition of "algorithm," an informal definition could be "a set of rules that precisely defines a sequence of operations." For some people, a program is only an algorithm if it stops eventually; for others, a program is only an algorithm if it stops before a given number of calculation steps.

A prototypical example of an algorithm is Euclid's algorithm to determine the maximum common divisor of two integers; an example (there are others) is described by the flow chart above and as an example in a later section.

Boolos & Jeffrey (1974, 1999) offer an informal meaning of the word in the following quotation:

No human being can write fast enough, or long enough, or small enough† ( †"smaller and smaller without limit ...you'd be trying to write on molecules, on atoms, on electrons") to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by ahuman who is capable of carrying out only very elementary operations on symbols.

The term "enumerably infinite" means "countable using integers perhaps extending to infinity." Thus Boolos and Jeffrey are saying that an algorithm implies instructions for a process that "creates" output integers from an arbitrary "input" integer or integers that, in theory, can be chosen from 0 to infinity. Thus an algorithm can be an algebraic equation such as y = m + n—two arbitrary "input variables" m and n that produce an output y. But various authors' attempts to define the notion (see more at Algorithm characterizations) indicate that the word implies much more than this, something on the order of (for the addition example):

Precise instructions (in language understood by "the computer") for a fast, efficient, "good" process that specifies the "moves" of "the computer" (machine or human, equipped with the necessary internally contained information and capabilities) to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = ... and "effectively" produce, in a "reasonable" time, output-integer y at a specified place and in a specified format.

The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systems come into being starting from a small set of axioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.

Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform (in a specific order) to carry out a specified task, such as calculating employees' paychecks or printing students' report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by aTuring-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987) and Gurevich (2000):

Minsky: "But we will also maintain, with Turing . . . that any procedure which could "naturally" be called effective, can in fact be realized by a (simple) machine. Although this may seem extreme, the arguments . . . in its favor are hard to refute".

Gurevich: "...Turing's informal argument in favor of his thesis justifies a stronger thesis: every algorithm can be simulated by a Turing machine ... according to Savage [1987], an algorithm is a computational process defined by a Turing machine".

Typically, when an algorithm is associated with processing information, data is read from an input source, written to an output device, and/or stored for further processing. Stored data is regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.

For some such computational process, the algorithm must be rigorously defined: specified in the way it applies in all possible circumstances that could arise. That is, any conditional steps must be systematically dealt with, case-by-case; the criteria for each case must be clear (and computable).

Because an algorithm is a precise list of precise steps, the order of computation will always be critical to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting "from the top" and going "down to the bottom", an idea that is described more formally by flow of control.

So far, this discussion of the formalization of an algorithm has assumed the premises of imperative programming. This is the most common conception, and it attempts to describe a task in discrete, "mechanical" means. Unique to this conception of formalized algorithms is the assignment operation, setting the value of a variable. It derives from the intuition of "memory" as a scratchpad. There is an example below of such an assignment.

For some alternate conceptions of what constitutes an algorithm see functional programming and logic programming. 

Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, programming languages or control tables (processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.

There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite state machine and state transition table), as flowcharts (see more at state diagram), or as a form of rudimentary machine code or assembly code called "sets of quadruples" (see more at Turing machine).

Representations of algorithms can be classed into three accepted levels of Turing machine description:

• 1 High-level description:

"...prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head."

• 2 Implementation description:

"...prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function."

• 3 Formal description:

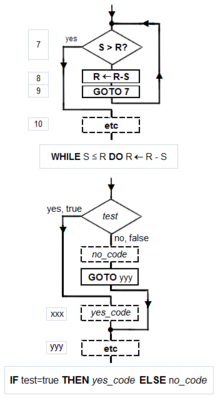
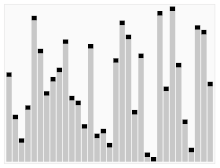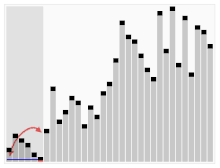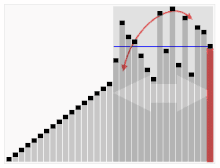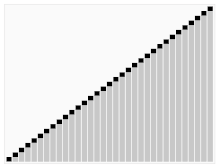
Most detailed, "lowest level", gives the Turing machine's "state table".

For an example of the simple algorithm "Add m+n" described in all three levels see Algorithm examples. 

Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brain implementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device. 

Flowchart examples of the canonicalBöhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (IF test=true THEN GOTO step xxx) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100,114).

In computer systems, an algorithm is basically an instance of logic written in software by software developers to be effective for the intended "target" computer(s), in order for the target machines to produce output from given input (perhaps null).

"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:

Knuth: ". . .we want good algorithms in some loosely defined aesthetic sense. One criterion . . . is the length of time taken to perform the algorithm . . .. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"

Chaitin: " . . . a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"

Chaitin prefaces his definition with: "I'll show you can't prove that a program is 'elegant'"—such a proof would solve the Halting problem (ibid).

Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This will be true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is . . . important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".

Unfortunately there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example of using Euclid's algorithm will be shown below.

Computers (and computors), models of computation: A computer (or human "computor"[25]) is a restricted type of machine, a "discrete deterministic mechanical device" that blindly follows its instructions. Melzak's and Lambek's primitive models reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.

Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability". Minsky's machine proceeds sequentially through its five (or six depending on how one counts) instructions unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution) operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[33] Rarely will a programmer have to write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing complete with only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT.

Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example". But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectively execute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't then for the algorithm to be effective it must provide a set of rules for extracting a square root.

This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).

But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters". When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" (division) instruction available rather than just subtraction (or worse: just Minsky's "decrement").

Structured programming, canonical structures: Per the Church-Turing thesis any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code" a programmer can write structured programs using these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language". Tausworthe augments the three Böhm-Jacopini canonical structures: SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE. An additional benefit of a structured program will be one that lends itself to proofs of correctness using mathematical induction.

Canonical flowchart symbols: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program of one). Like program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only 4: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm-Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles but only if a single exit occurs from the superstructure. The symbols and their use to build the canonical structures are shown in the diagram.

An animation of the quicksort algorithmsorting an array of randomized values. The red bars mark the pivot element; at the start of the animation, the element farthest to the right hand side is chosen as the pivot.

One of the simplest algorithms is to find the largest number in an (unsorted) list of numbers. The solution necessarily requires looking at every number in the list, but only once at each. From this follows a simple algorithm, which can be stated in a high-level description English prose, as:

next