Аксиальный вектор (англ. axial, осевой) или псевдовектор, величина, преобразующаяся как вектор при операциях поворота, но, в отличие от вектора, не меняющая свой знак при инверсии (обращении знака) координат. Простейшим примером А.в. в трёхмерном пространстве является векторное произведение, например, в механике — момент импульса 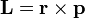, в четырёхмерном пространстве —аксиальный ток.

При преобразовании координат координаты А.в. получают домножением на дополнительный множитель (-1) по сравнению с преобразованием координат истинных (иначе называемых полярными) векторов, если базис меняет ориентацию (например, зеркальное отражение). Это, наряду с псевдоскаляром, частный случай псевдотензора. Графически изображенный псевдовектор при таком изменении координат меняет направление на противоположное.

• В геометрии наиболее употребительным применением псевдовектора может быть представление с его помощью трехмерного бесконечно малого поворота. Вероятно(?), термин А.в. происходит именно отсюда, так как псевдовектор определяет ось поворота (ее направление), но только с точностью до множителя (±1), с направлением же вращения связан условным произвольным выбором правого базиса, в отличие от истинного (полярного) вектора, представляющего направленный отрезок (или параллельный перенос) вполне определенно и однозначно заданного точками начала и конца.

Обычный путь порождения псевдовекторов это псевдовекторные операции, наиболее обычной, если не единственной из употребительных в трехмерном случае является векторное произведение (так как оно в обычной координатной записи включает псевдотензор Леви-Чивиты) и операции, содержащие векторное произведение (например, ротор и т.п.) или нечетное их количество. Псевдовекторная операция порождает из истинных векторов и скаляров псевдовекторы и псевдоскаляры.

Так, при умножении истинного вектора на истинный вектор — получается в скалярном произведении истинный скаляр, а в векторном произведении — псевдовектор. При умножении истинного вектора на псевдовектор — получается в скалярном произведении псевдоскаляр, а в векторном произведении истинный вектор. При перемножении двух псевдовекторов — получаются соответственно истинный скаляр и псевдовектор.

В физических теориях, за исключением таких, в которых присутствует явное и в принципе наблюдаемое нарушение зеркальной симметрии пространства, псевдовекторы могут присутствовать в промежуточных величинах, но в конечных, наблюдаемых — множители (-1) при зеркальных отражениях координат должны уничтожаться, встречаясь в произведениях четное количество раз (четное количество псевдовекторных + псевдоскалярных + других псевдотензорных множителей).

• Например, в классической электродинамике индукция магнитного поля — псевдовектор, так как порождается псевдовекторной операцией, например jxr в законе Био-Савара, но сама эта величина (псевдовектор) определена в принципе с точностью до условного множителя, который может быть выбран +1 или −1. Однако реально наблюдаемая величина — ускорение заряда под действием магнитного поля — при своем вычислении содержит еще одну псевдовекторную операцию vxB в выражении для силы Лоренца, дающую еще один условный множитель ±1, равный первому, в ответе же произвол пропадает, так как произведение ±1·(±1) дает просто 1.

• В механике наиболее часто встречающаяся псевдовекторная величина — вектор угловой скорости и связанные с нею (например, момент импульса).