Информационный центр "Центральный Дом Знаний"
|
Алгоритм ДиксонаАлгоритм
Диксона, алгоритм факторизации,
использующий в своей основе идею Лежандра,
заключающуюся в поиске пары целых
чисел x и y таких, что Метод Диксона является обобщением метода Ферма.
Пусть задано
подмножество простых чисел
Каждому Β-гладкому
числу сопоставляется вектор показателей
из разложения
Если теперь
подобрать такое множество различных Β-гладких
чисел
то для
произведения
где y определяется как
Описание алгоритма:
Среднюю временную арифметическую сложность А.Д. можно оценить выражением
где
Возьмем в
качестве M величину
Отсюда следует, что трудоемкость А.Д. оценивается следующим образом
Лит.: Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. 2003. Стр. 78-83. Черемушкин А. В. Лекции по арифметическим алгоритмам в криптографии. 2002. Стр. 77-80. |
Loading
| |||||||||||||||||||||||||||||||||||||||||||||||||||||


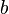 до
тех пор, пока не будет найдено
до
тех пор, пока не будет найдено  ,
являющихся Β-гладкими.
,
являющихся Β-гладкими. .
.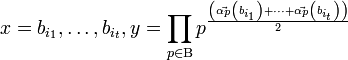 .
. .
Если это так, то повторить процедуру
генерации. Если нет, то найдено
нетривиальное разложение:
.
Если это так, то повторить процедуру
генерации. Если нет, то найдено
нетривиальное разложение: